
Explicação dos símbolos do diagrama de Venn
Tempo de leitura: cerca de 5 minutos
Tópicos:
Símbolos de diagramas de Venn
∪: União de dois conjuntos. Um diagrama de Venn completo representa a união de dois conjuntos.
∩: Interseção de dois conjuntos. A interseção mostra quais itens são compartilhados entre as categorias.
Ac: Complemento de um conjunto. O complemento é o que não está representado em um conjunto.
Agora vamos falar sobre diagramas de Venn — e saiba que não tem nada a ver com aqueles que você usava na escola. Estamos falando dos elementos visuais criados por profissionais sérios para representar ideias matemáticas complexas.
Diagramas de Venn são representações visuais de conjuntos matemáticos — ou coleções de objetos — estudados por uma vertente da lógica chamada teoria dos conjuntos. A teoria dos conjuntos é um dos sistemas fundamentais da matemática, e nos ajudou a desenvolver um entendimento moderno do infinito e de números reais.
Pesquisadores e matemáticos desenvolveram uma linguagem e um sistema de notação sobre a teoria dos conjuntos. Se quiser saber mais, recomendamos se familiarizar com estes símbolos de diagramas de Venn.
Este guia vai orientá-lo na criação de um diagrama de Venn, e explicaremos os símbolos ao longo do caminho. Vamos usar o Lucidchart para criar nossos exemplos por ser uma plataforma prática e gratuita. Para acompanhar ou criar seu próprio diagrama de Venn, basta clicar abaixo e criar uma conta gratuita. Agora vamos lá!
Diagramas de Venn e teoria dos conjuntos
Existem mais de 30 símbolos usados na teoria dos conjuntos, mas você precisa conhecer apenas três para entender as noções básicas. Depois de dominar esses, fique à vontade para se aprofundar ainda mais.
Conjunto União: ∪
Cada círculo ou elipse representa uma categoria. A união de dois conjuntos é representada por ∪. (Não confunda este símbolo com a letra “u”.)
Este é um diagrama de Venn de dois círculos. O círculo verde é A e o círculo azul é B. O diagrama de Venn completo representa a união de A e B, ou A ∪ B. Clique na imagem para utilizar este diagrama como modelo.
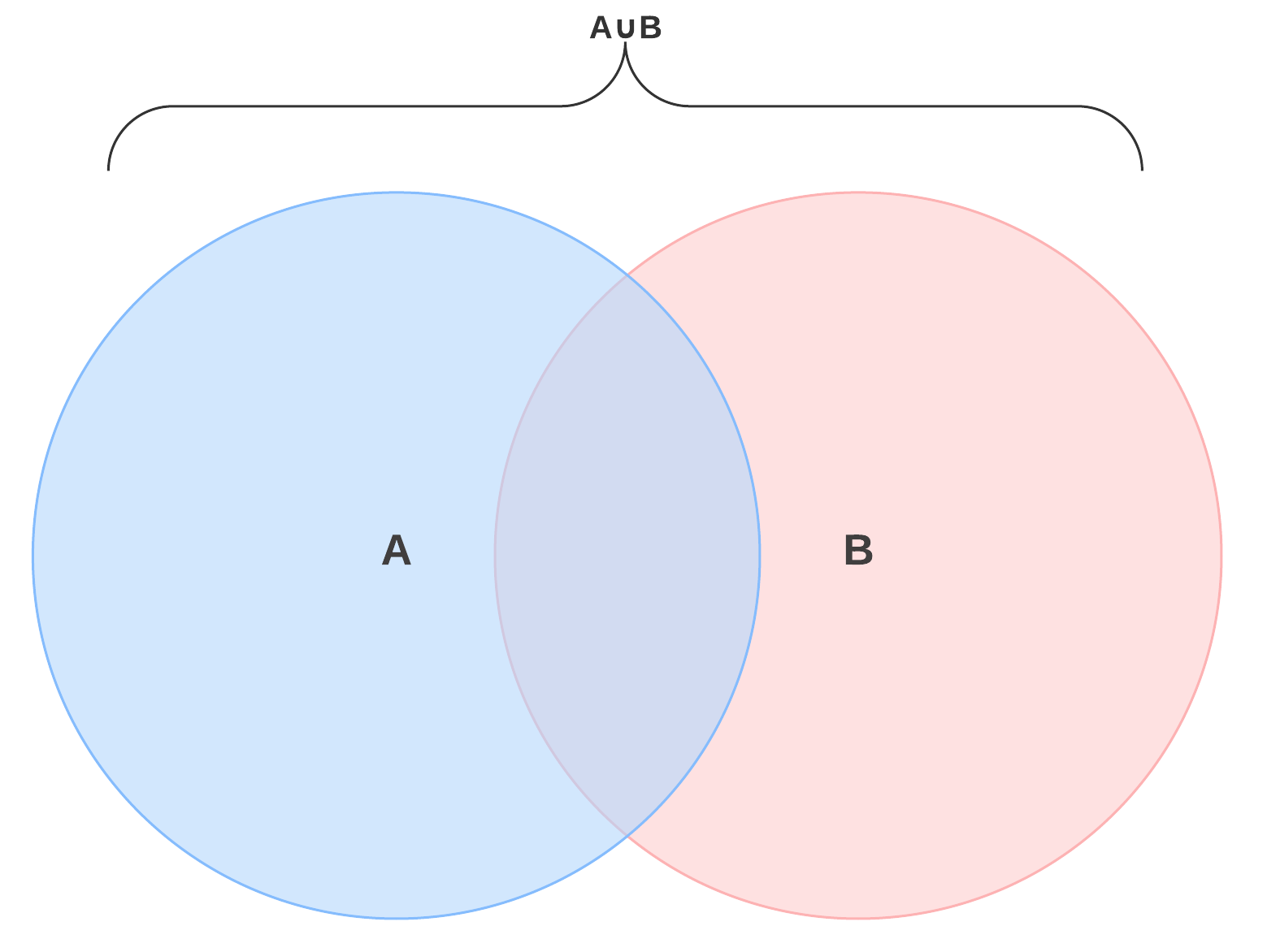
Na prática, como seria a união de dois conjuntos? O conjunto A poderia representar um grupo de pessoas que tocam piano. O conjunto B poderia representar guitarristas. A ∪ B representa aqueles que tocam piano, guitarra ou ambos.
Conjunto Interseção: ∩
Ao criar um diagrama de Venn, consideramos a interseção de dois conjuntos, ou seja, os itens compartilhados entre as categorias. Neste diagrama, a área verde-azulada (onde há sobreposição de azul e verde) representa a interseção de A e B, ou A ∩ B.
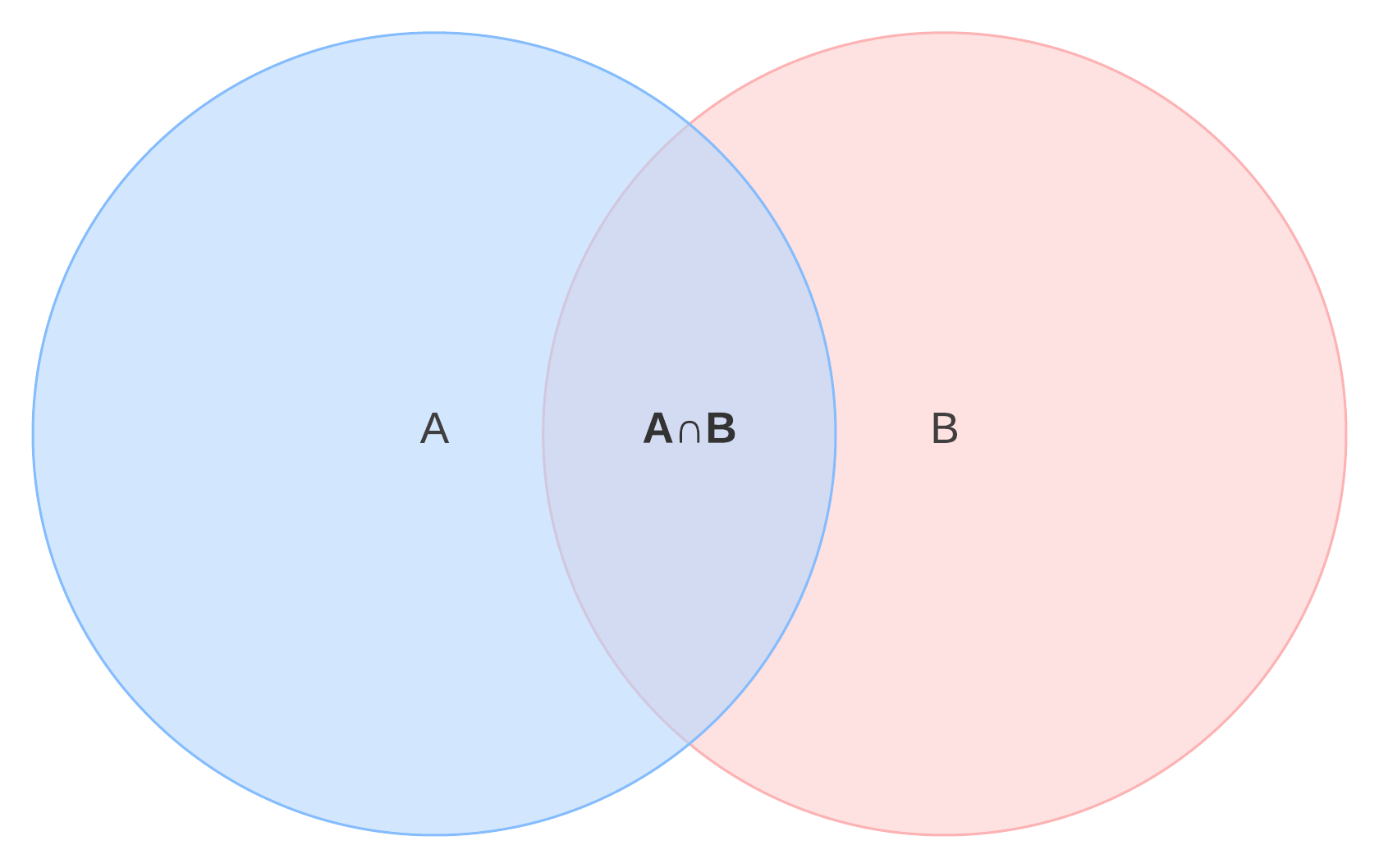
Para dar seguimento ao exemplo, a interseção de tocadores de piano e guitarra inclui aqueles que dominam ambos os instrumentos.
Conjunto Complementar: Ac
Ao criar um diagrama de Venn, também consideramos aquilo que não é representado em um conjunto. Este é o complemento de um conjunto, ou Ac, para o conjunto A.
O complemento absoluto de um conjunto é tudo o que não está incluído no conjunto. Isso significa que, em dado universo (U, a própria letra, neste caso), tudo o que existe no universo, exceto para A, é o complemento absoluto de A em U. Isso pode ser representado pela equação Ac = U \ A.
Veja abaixo um diagrama do Lucidchart para o complemento absoluto de A em U. A seção cinza mostra tudo fora de A. No caso do instrumento musical, seriam todos que não tocam piano.
Um diagrama de Venn de comida fast-food ilustrando a teoria dos conjuntos
Para ajudá-lo a entender melhor a aplicação prática da teoria dos conjuntos, veja um exemplo. Vamos começar com uma pesquisa sobre as preferências de comida fast-food de três pessoas. Essas três pessoas, a quem vamos atribuir A, B e C, indicam quais restaurantes preferem. Um diagrama de três círculos cobre todas as possibilidades: que um restaurante será escolhido por nenhum dos respondentes, por um, por dois ou pelos três.
Veja os resultados:
| Restaurante | T | B | C |
|---|---|---|---|
| McDonald's | x | x | |
| Wendy's | x | x | |
| Burger King | |||
| In-N-Out | x | x | |
| Taco Bell | x | x | |
| KFC | |||
| A&W | |||
| Chick-fil-A | x | x | x |
Agora é hora de criar um diagrama de Venn representando os resultados. Vamos começar com este modelo abaixo. Ele utiliza o símbolo que explicamos, ∩, para exibir a interseção entre dois e três conjuntos. Existem oito regiões que nossos restaurantes poderiam ocupar.
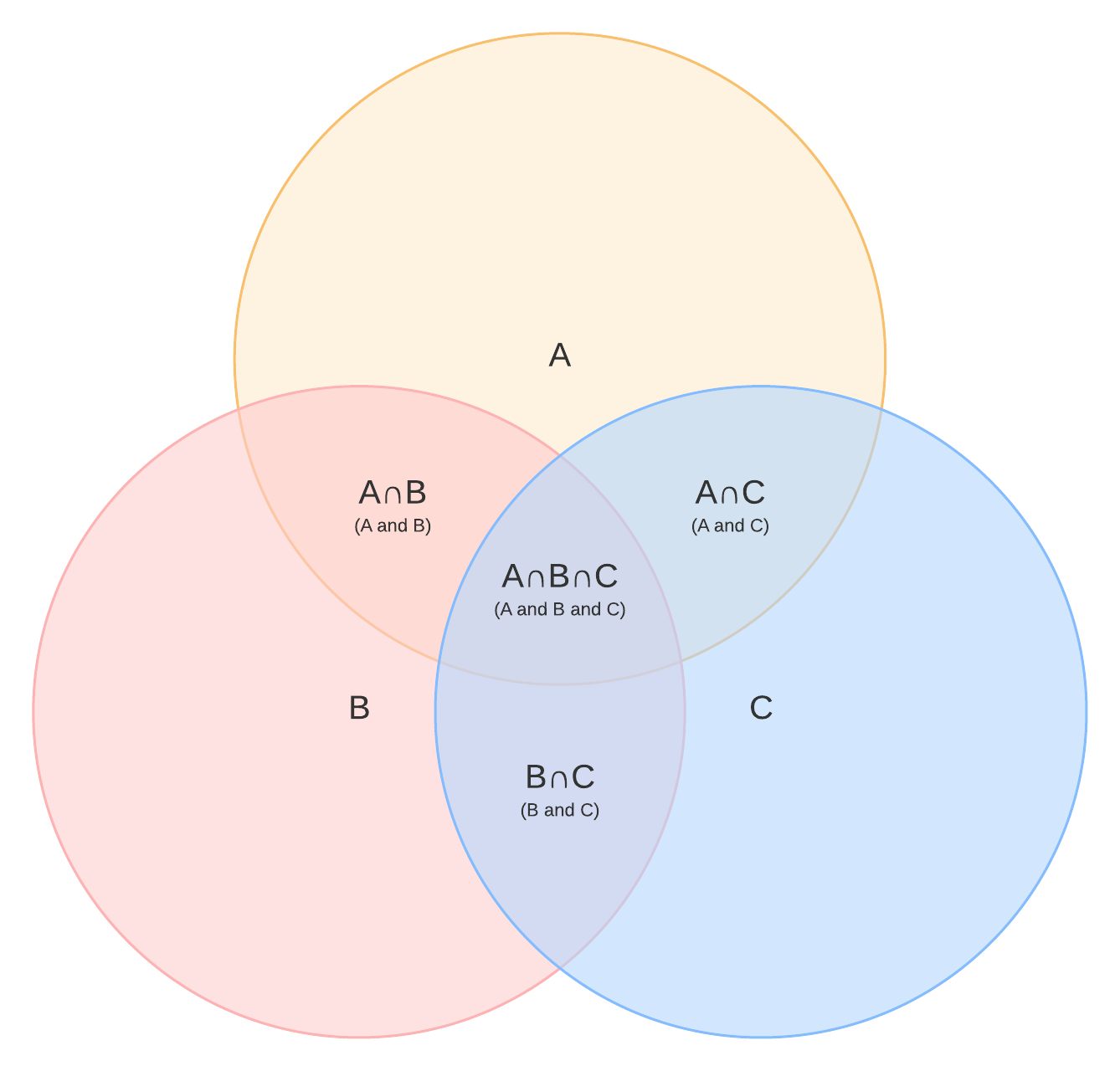
Agora vamos preencher nosso diagrama de Venn de acordo com os resultados. Em A ∩ B, temos o Wendy's, porque o respondente A e o respondente B o escolheram. O Burger King não foi escolhido por ninguém, mas existe no universo de restaurantes fast-food; portanto, é colocado no espaço em branco fora do diagrama. A interseção dos três, A ∩ B ∩ C, tem o Chick-fil-A, uma vez que os três respondentes o escolheram.
O diagrama final fica assim:
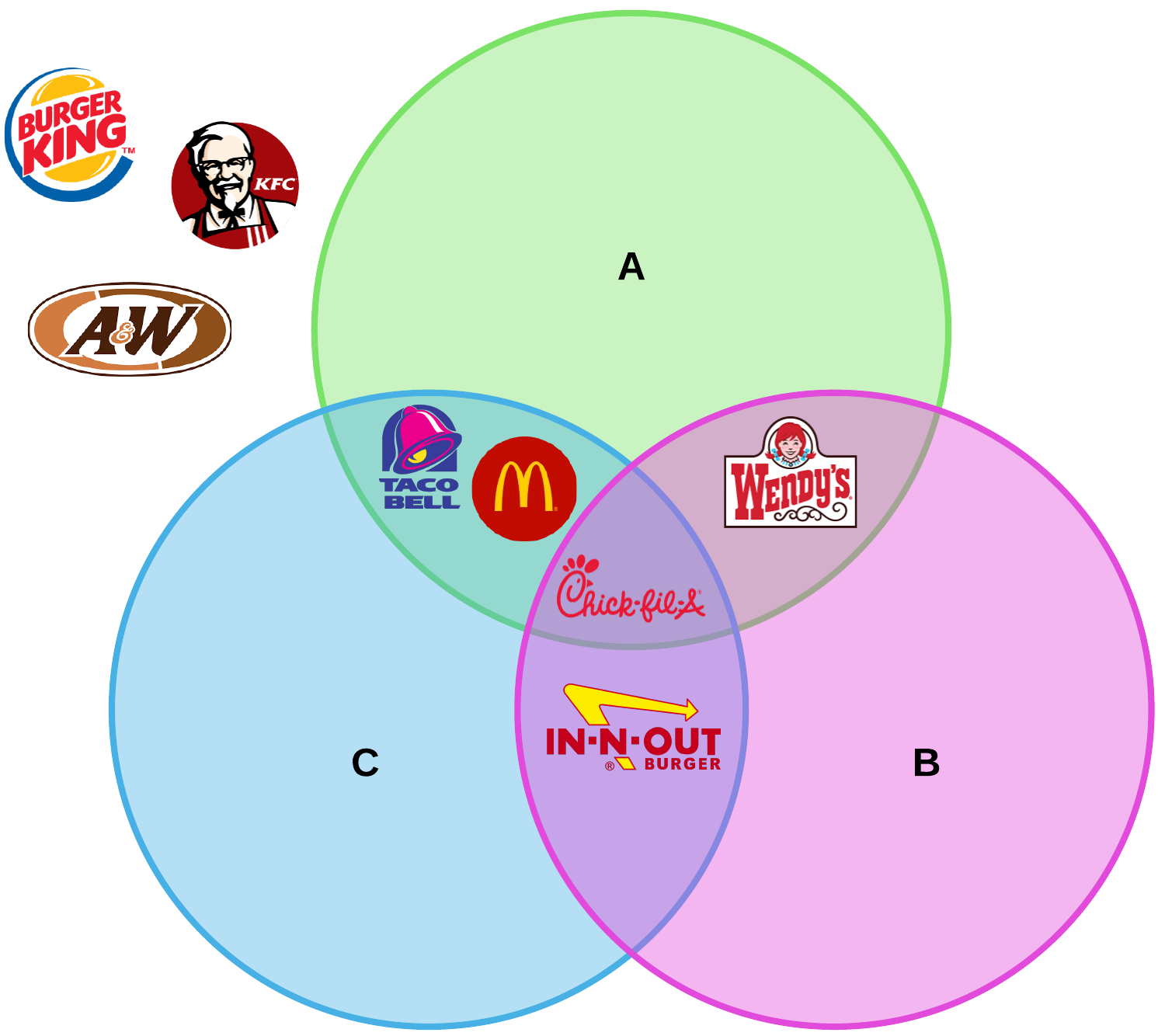
Agora temos um recurso visual para nos ajudar a escolher onde estas três pessoas deveriam ir para almoçar!
Agora que você conheceu um diagrama de Venn na prática, veja um exemplo personalizável para criar o seu próprio!
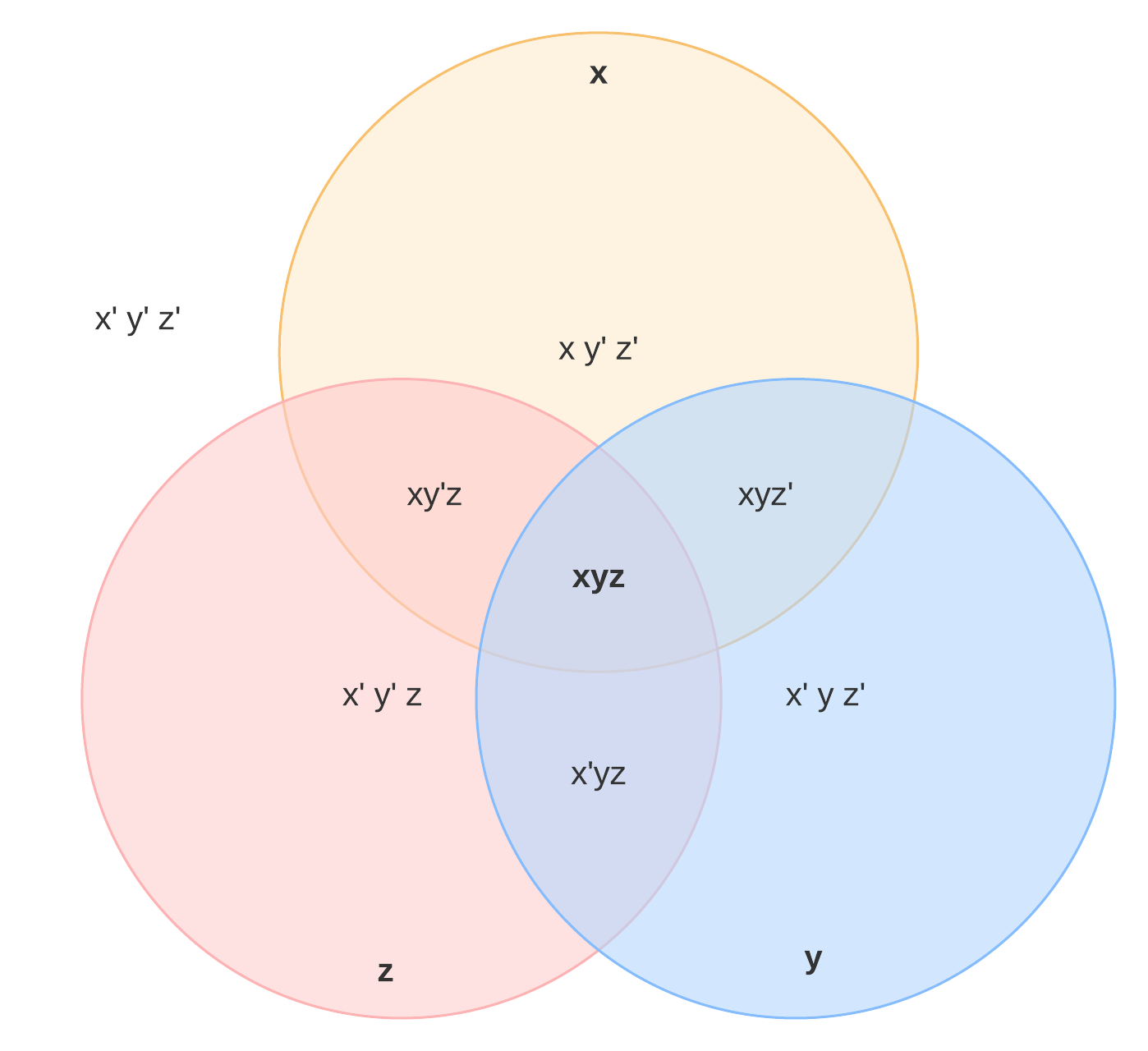
Agora que você conhece os símbolos do diagrama de Venn, leia mais para aprender como criar um!
Veja comoLeitura complementar sobre símbolos de diagramas de Venn
Se quiser saber mais sobre a teoria dos conjuntos e como criar diagramas de Venn de alta qualidade, existem várias fontes de informação. Por exemplo, a Enciclopédia Stanford oferece uma introdução à Teoria dos conjuntos básica.
Para saber mais sobre a história dos diagramas de Venn, leia nossa página “O que é um diagrama de Venn?” Embora John Venn tenha popularizado a representação da teoria dos conjuntos com círculos sobrepostos, as ideias e os símbolos nos diagramas, na verdade, foram criados antes.
Uma breve observação
Se você está acompanhando isso no Lucidchart, já entendeu que é a solução ideal para criar diagramas de Venn. Como você está editando na nuvem, você pode colaborar com colegas, importar imagens e compartilhar seus diagramas digitalmente ou por material impresso com facilidade.

Veja como o nosso gerador de diagramas de Venn funciona.
Saiba maisSobre: Lucidchart
O Lucidchart, um aplicativo de diagramação inteligente que roda na nuvem, é um componente central da Suíte de colaboração visual da Lucid Software. Essa solução intuitiva de nuvem oferece às equipes a possibilidade de colaborar em tempo real para criar fluxogramas, mockups, diagramas UML, mapas de jornada do cliente e muito mais. O Lucidchart impulsiona as equipes para uma construção mais ágil do futuro. A Lucid tem orgulho de atender às principais empresas de todo o mundo, incluindo clientes como Google, GE e NBC Universal, e 99% das empresas da Fortune 500. A Lucid faz parceria com líderes do setor, como Google, Atlassian e Microsoft. Desde a inauguração, a Lucid recebeu vários prêmios por seus produtos e negócios e pela cultura no local de trabalho. Veja mais informações em lucidchart.com/pt.
