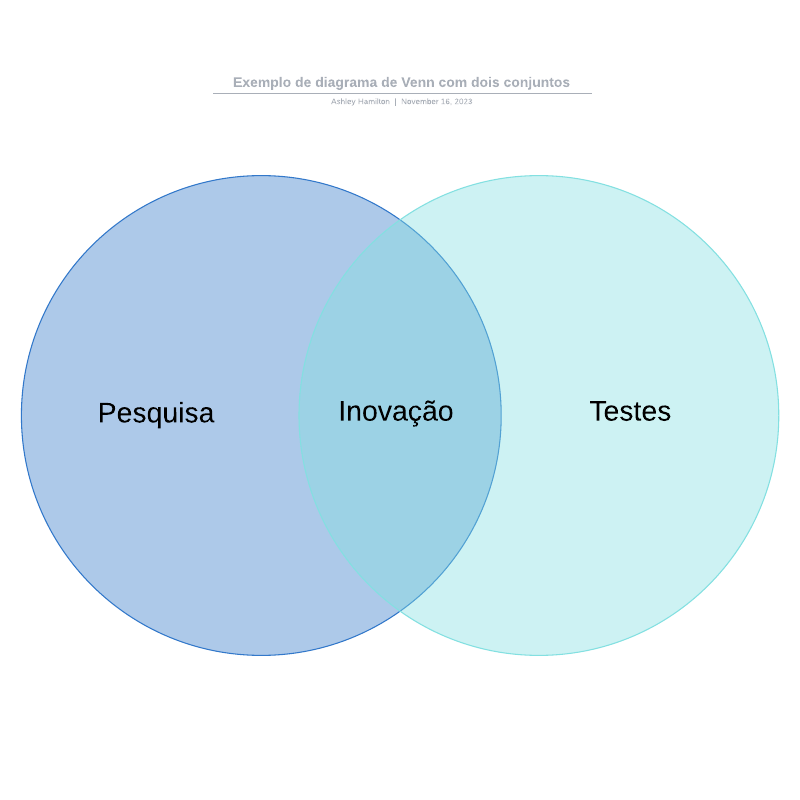
O que é um diagrama de Venn?
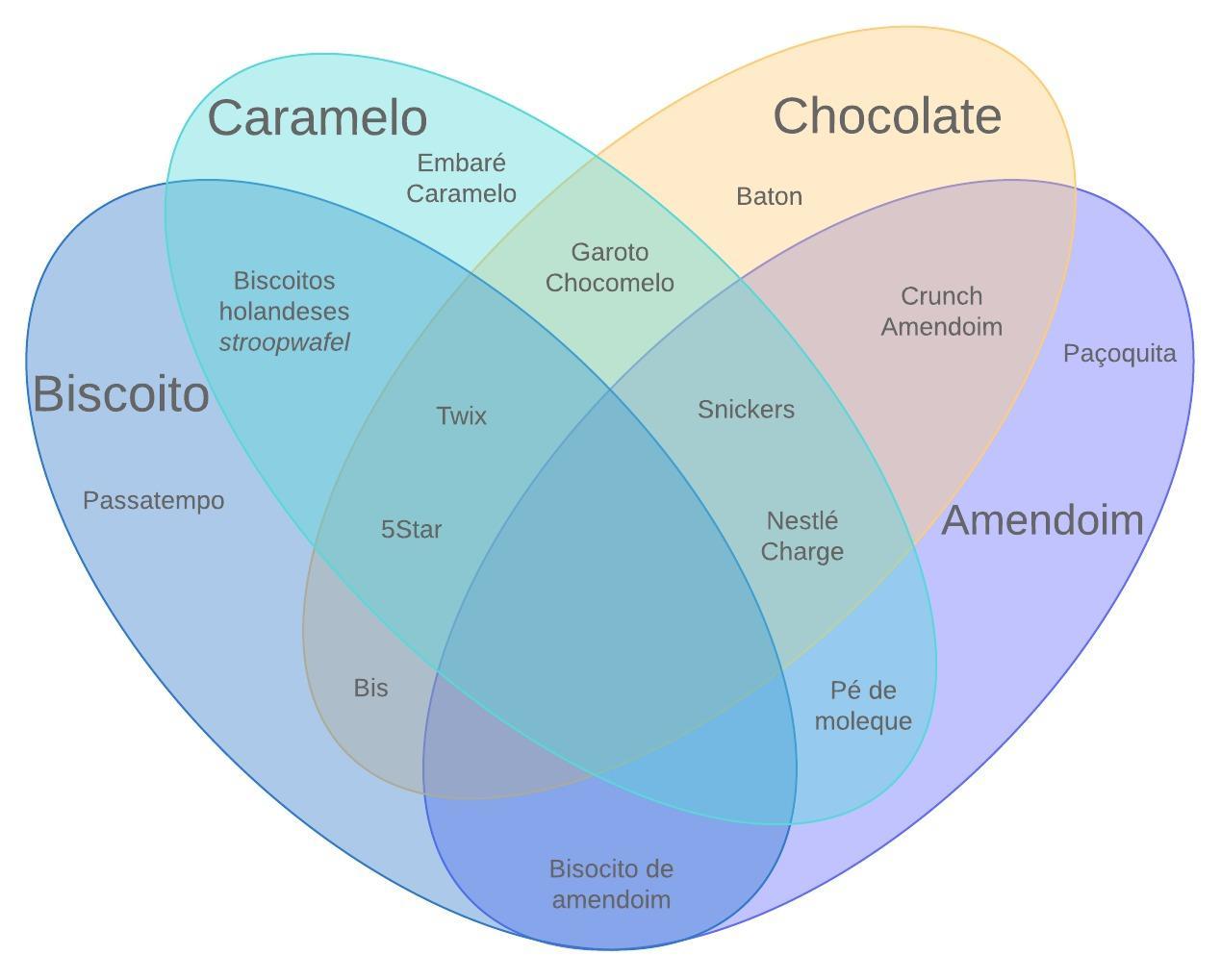
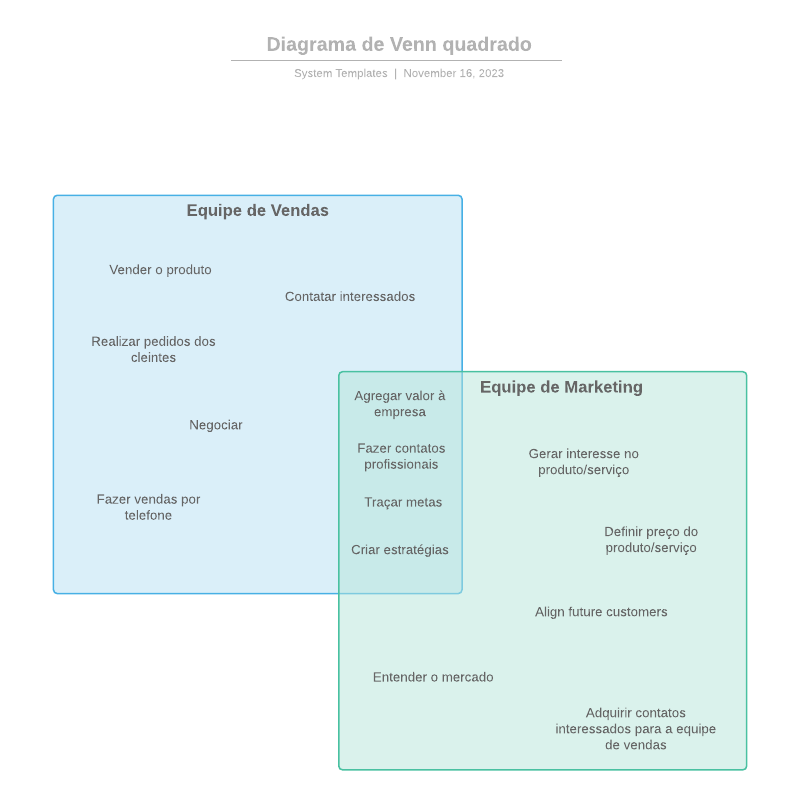
Um Diagrama de Venn usa círculos sobrepostos ou outras formas para ilustrar as relações lógicas entre dois ou mais conjuntos de itens. Muitas vezes, eles servem para organizar graficamente as coisas, destacando como os itens são semelhantes e diferentes. Os Diagramas de Venn, também chamados de Diagramas de Conjuntos ou Diagramas Lógicos, são amplamente usados em matemática, estatística, lógica, ensino, idiomas, ciência da computação e negócios. O primeiro contato de muitas pessoas com eles acontece na escola ao estudar matemática ou lógica, uma vez que os Diagramas de Venn se tornaram parte da "nova grade de matemática" na década de 1960. Eles podem ser simples diagramas envolvendo dois ou três conjuntos de alguns elementos, ou podem ser bastante sofisticados, incluindo apresentações em 3D, à medida que avançam para seis ou sete conjuntos e além. Eles são usados para refletir e descrever como os itens se relacionam uns com os outros dentro de um "universo" ou segmento específico. Os Diagramas de Venn permitem que os usuários visualizem dados de maneiras claras e poderosas, e, consequentemente, são usados geralmente em apresentações e relatórios. Eles estão intimamente relacionados aos Diagramas de Euler, que se distinguem por omitir os conjuntos se não houver itens neles. Os Diagramas de Venn mostram as relações mesmo que o conjunto esteja vazio.



Aprenda a usar o Lucidchart em 3 minutinhos
- Comece a criar seu primeiro Diagrama de Venn com um modelo pronto para editar, uma tela em branco ou um documento importado.
- Adicione formas, conecte linhas e escreva texto.
- Ajuste o estilo e a formatação de seu diagrama.
- Use a função Localizar Recurso para encontrar tudo o que você precisa.
- Compartilhe seu gráfico de Gantt com sua equipe e dê início à colaboração.
Histórico
Os Diagramas de Venn são nomeados em homenagem ao lógico britânico John Venn. Ele escreveu sobre os diagramas em um artigo de 1880 intitulado "Sobre a Representação Diagramática e Mecânica de Proposições e Raciocínios" na Philosophical Magazine e Journal of Science.

Mas as raízes deste tipo de diagrama remontam há muito mais tempo, pelo menos 600 anos. Em meados de 1200, o filósofo e lógico Ramon Llull (às vezes soletrado Lull) de Maiorca usou um tipo semelhante de diagrama, escreveu a autora M.E. Baron em um artigo de 1969 que traçava a sua história. Ela também creditou o matemático e filósofo alemão Gottfried Wilhelm von Leibniz por desenhar diagramas semelhantes no final de 1600.


Em meados de 1700, o matemático suíço Leonard Euler (pronunciado Oy-ler) inventou o que veio a ser conhecido como o Diagrama de Euler, o precursor mais direto do Diagrama de Venn. Na verdade, John Venn se referia a seus próprios diagramas como Círculos Eulerianos, e não como Diagramas de Venn. O termo Diagramas de Venn foi publicado pela primeira vez pelo filósofo americano Clarence Irving (C.I.) Lewis em seu livro de 1918, Uma Pesquisa da Lógica Simbólica.
Os Diagramas de Venn continuaram a evoluir ao longo dos últimos 60 anos com avanços dos especialistas David W. Henderson, Peter Hamburger, Jerrold Griggs, Charles E. "Chip" Killian e Carla D. Savage. Seu trabalho dizia respeito a Diagramas de Venn simétricos e sua relação com números primos, ou números indivisíveis por outros números, exceto 1 e o próprio número. Um desses diagramas simétricos, baseado no número primo 7, é amplamente conhecido nos círculos matemáticos como Victoria.
Outros nomes notáveis no desenvolvimento de Diagramas de Venn são A.W.F. Edwards, Branko Grunbaum e Henry John Stephen Smith. Entre outras coisas, eles mudaram as formas nos diagramas para permitir uma representação mais simples dos Diagramas de Venn em cada vez mais conjuntos.
Um simples exemplo
Digamos que nosso universo é animais de estimação, e queremos comparar com qual tipo de animal de estimação nossa família pode concordar.
O conjunto A contém minhas preferências: cão, pássaro, hamster.
O conjunto B contém preferências do membro B da família: cão, gato, peixe.
O conjunto C contém as preferências do membro C da família: cão, gato, tartaruga, cobra.
A sobreposição, ou interseção, dos três conjuntos contém apenas cão. Parece que vamos comprar um cão.
Naturalmente, os Diagramas de Venn podem se tornar muito mais envolventes do que isso, pois são usados extensivamente em vários campos.
Propósito e benefícios
- Organizar visualmente as informações para ver a relação entre conjuntos de itens, como pontos comuns e diferenças. Estudantes e profissionais podem usá-los para pensar sobre a lógica por trás de um conceito e descrever as relações para comunicação visual. Este objetivo pode variar de elementar a altamente avançado.
- Comparar duas ou mais escolhas e ver claramente o que elas têm em comum e o que elas têm de diferente. Isso pode ser feito para escolher um produto ou serviço importante para comprar.
- Resolver problemas matemáticos complexos. Presumindo que você seja um matemático, é claro.
- Comparar conjuntos de dados, encontrar correlações e prever probabilidades de certas ocorrências.
- Entender a lógica por trás de declarações ou equações, como a lógica booleana por trás de uma pesquisa de palavras envolvendo declarações "ou" e "e" e como elas são agrupadas.
Usos em diferentes segmentos
- Matemática: os Diagramas de Venn são muito usados na escola para ensinar conceitos matemáticos básicos, como conjuntos, uniões e interseções. Eles também são usados em matemática avançada para resolver problemas complexos e foram mencionados extensivamente em revistas acadêmicas. A teoria de conjuntos representa um ramo inteiro da matemática.
- Estatísticas e probabilidade: especialistas em estatística usam o Diagramas de Venn para prever a probabilidade de certas ocorrências. Isso está relacionado ao campo da análise preditiva. Diferentes conjuntos de dados podem ser comparados para encontrar graus de comunalidade e diferenças.
- Lógica: os Diagramas de Venn são usados para determinar a validade de argumentos e conclusões específicos. No raciocínio dedutivo, se as premissas forem verdadeiras e a forma do argumento estiver correta, então a conclusão deve ser verdadeira. Por exemplo, se todos os cães são animais, e nosso mascote Mojo é um cão, então Mojo tem que ser um animal. Se atribuirmos variáveis, digamos que os cães são C, os animais são A e Mojo é B. Em forma de argumento, dizemos: todos os C são A. B é C. Portanto, B é A. Um diagrama relacionado em lógica é chamado de Tabela da Verdade, que coloca as variáveis em colunas para determinar o que é logicamente válido. Outro diagrama relacionado é chamado de Diagrama de Randolph, ou Diagrama R, em homenagem ao matemático John F. Randolph. Ele usa linhas para definir conjuntos.
- Linguístico: os Diagramas de Venn foram usados para estudar as semelhanças e diferenças entre os idiomas.
- Ensino da compreensão de leitura: os professores podem usar Diagramas de Venn para melhorar a compreensão de leitura de seus estudantes. Os estudantes podem desenhar diagramas para comparar e contrastar ideias sobre as quais estão lendo.
- Ciência da computação: os programadores podem usar Diagramas de Venn para visualizar linguagens de computador e hierarquias.
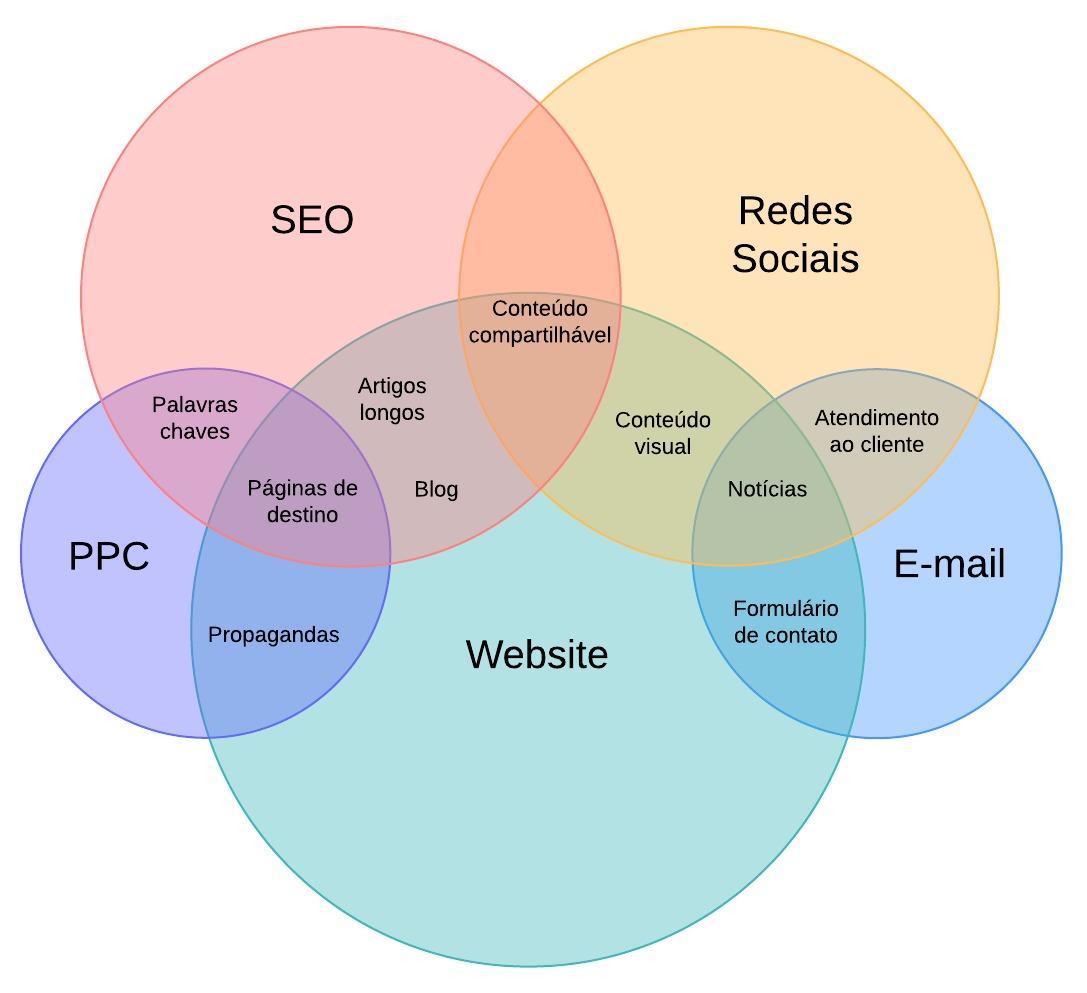
- Negócios: os Diagramas de Venn podem ser usados para comparar e contrastar produtos, serviços, processos ou praticamente qualquer coisa que pode ser representada em conjuntos. Eles são uma ferramenta de comunicação eficaz para ilustrar essa comparação.
Glossário do diagrama de Venn
| Conjunto | Uma coleção de coisas. Dada a versatilidade dos Diagramas de Venn, as coisas podem realmente ser qualquer coisa. As coisas podem ser chamadas de itens, objetos, membros ou termos similares. |  |
| União | Todos os itens nos conjuntos. |  |
| Interseção | Os itens que se sobrepõem nos conjuntos. Às vezes é chamada de subconjunto. |  |
| Diferença simétrica de dois conjuntos | Tudo, exceto a interseção. |  |
| Complemento absoluto | Tudo que não está no conjunto. |  |
| Complemento relativo | Em um conjunto, mas não no outro. |  |
| Diagrama de Venn dimensionado | Também chamado de Área Proporcional. Os círculos (ou outras formas) são dimensionados pela representação proporcional do todo. |  |
| Triângulo Reuleaux | Forma composta pela interseção de três circulares ou formas, como em um Diagrama de Venn. |  |
| Notações de conjuntos |
Os conceitos ilustrados nos Diagramas de Venn são expressos com notações matemáticas, como aquelas que representam conjuntos e subconjuntos (entre parênteses), uniões (com um símbolo em forma de U) e interseções (com um símbolo em forma de U invertido). | |
| Teoria dos conjuntos | O duradouro ramo da matemática que lida com conjuntos. |
Mudando de assunto: os diagramas de Venn chegam à telinha
Não são muitos os diagramas que atravessaram a barreira para a cultura popular, mas o famoso Diagrama de Venn conseguiu.
- Drama: no programa de TV NUMB3RS da CBS, produzido de 2005 a 2010, o gênio da matemática Charles Eppes usa um Diagrama de Venn para determinar quais suspeitos correspondem a uma descrição e têm um histórico de violência.
- Comédia: no Late Night da NBC com Seth Meyers, o comediante tem uma rotina recorrente chamada de "Diagramas de Venn", onde ele compara dois itens aparentemente não relacionados para encontrar suas semelhanças engraçadas (é o que ele espera.)
Passos para desenhar e usar um diagrama de Venn básico
- Determine seu objetivo. O que você está comparando, e por quê? Isso lhe ajudará a definir os conjuntos.
- Discuta e liste os itens em seus conjuntos, seja em papel ou com uma plataforma, como o Lucidchart.
- Agora, use o diagrama para comparar e contrastar os conjuntos. Você pode ver as coisas de novas maneiras e ser capaz de fazer observações, escolhas, justificativas ou decisões.